1.
Recently I was having a discussion in the comments section of the Astral Codex Ten blog (to the people who haven’t heard of it: I highly recommend reading one or two of Scott’s articles) about how it’s possible for two positively associated in reality traits A and B to show a zero or even negative correlation if we’re selecting our sample from a group based on some other trait C that is influenced by both of them:

In fancy statistics terminology this sort of situation is called a collider. If we control for the collider in any way then our standard linear regression estimate of the true effect of A on B will be changed.
The simplest example of a collider is a bag which is independently filled with between 0-100g of lemon drops and 0-100g of butterscotch candy. On its own there is no relationship between the amount of lemon drops and the amount of butterscotch in a bag and knowing one tells you nothing about the other. However now suppose we knew the weight of the bag. In this case by subtracting the amount of lemon drops in the bag we immediately know the amount of butterscotch present too.
So if our sample e.g. consisted of just bags with a net weight of 150g then we’d find that the amount of lemon drops perfectly predicts the amount of butterscotch leading to correlation = -1. This correlation gives a very false impression about the true relationship between the amounts of lemon drops and butterscotch in bags.
In fact things are even worse than that. There’s nothing special about the number 150g in my last paragraph. For any fixed weight of the bag it’s true that if our sample consists of bags with that exact weight we’ll find the correlation to equal -1. Hence leading to the somewhat counterintuitive result that for every possible weight of the bag there is a negative link between the amounts of lemon drops and butterscotch, however taken overall there is no dependence at all! This is an example of Simpson's Paradox which is very interesting in its own right but not exactly what this post is about so we’ll leave it there.
Formally we’d describe this situation as “the weight of the bag acts as a collider for the relationship between how many grams of lemon drops there are vs how many grams of butterscotch”. Without controlling for it we see our expected result of zero link between the two quantities but when we do control it leads to the Spurious Correlation we just saw. Hence why we have the common refrain “don’t condition on a collider” (unless you can block the path between treatment and outcome through some other way, but now we’re getting too complex and exactly how and when we can do that is outside the scope of this post).
Note that “conditioning on a collider” doesn’t just mean choosing a subset where all samples have the same fixed value of the collider. It means any selection process which depends on the value of the collider at all. For instance, restricting your sample to only “heavy” bags weighing > 100g would still result in a case where knowing the amount of lemon drops tells you information about the amount of butterscotch. In such a case if you have a bag with 10g of lemon drops you immediately know that it must have >= 90g of butterscotch. This time our info isn’t as precise as in the fixed weight case so our measured correlation will have a magnitude less than 1 but still be negative. We can see this graphically by plotting the “allowed” region in the lemon drop-butterscotch space and seeing that this looks like a top right triangle, which has a non-zero correlation between the things plotted.
2.
My discussion on ACX started after Scott quoted one of my comments in his highlights roundup about how we can have cases where a measure of job suitability can be positively correlated to job performance in reality but still show up as being uncorrelated to job performance among the people who were hired. I gave the example of how height is uncorrelated with performance in the NBA:
» “As I said above, if you read the actual case, the facts were that the test did not predict success at the job. This turns out to be very common.”
This does not mean the test isn't a good test in the sense that it doesn't measure job performance. See how there is no correlation between a players [sic] height in the NBA and how well they perform. This is because if there was a correlation then selectors would be leaving money on the table and they could improve their selection for the coming year by increasing the weighting on height (compared to everything else), which would in turn reduce the amount of correlation. Rinse and repeat until there is no correlation left.
The test not predicting job performance could equivalently mean that Duke Power had a very well calibrated way to choose their employees where they were prefectly capturing the information from the apitutde [sic] test compared to all the other factors involved in hiring. Indeed the fact that this turns out to be very common suggests to me that this is going on here (and elsewhere).
Some people asked for a source about this claim, especially because there’s a paper that looked at FIBA instead of the NBA and found that height did have a correlation to performance at the basketball world cups. I’ve put my reply about this in its own section at the end of the post to avoid disrupting the main flow of the article.
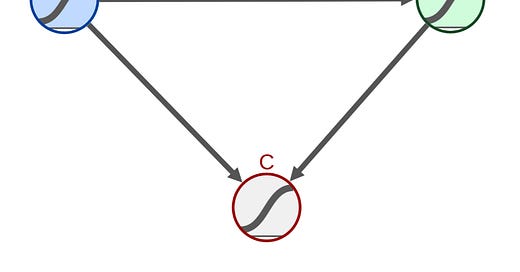
We can come up with a model for how we expect test performance to affect job performance. In this case the Directed Acyclic Graph (DAG) looks like this:
We see that both Job performance (technically this is job performance *if* they were hired) and getting hired are a combination of two things: Test Performance and Other factors, which includes things like conscientiousness, workplace fit etc. Technically there’s also noise in both whether someone got hired (maybe their hiring manager discriminated against them) and how well they perform on the job (maybe they got sick so did much worse than otherwise) but for simplicity’s sake we’ll assume they aren’t present. Adding them in would reduce the magnitude of correlations across the board but otherwise not change the main thrust of what we’re trying to do here.
We assume that test performance and other factors are in reality uncorrelated (as in the classic Berkson’s paradox). Furthermore we stipulate whether or not a worker gets hired is based upon how well they did in the general ability test as well as the other factors. In reality it won’t be possible for hiring managers to be able to measure or select on literally all the other factors which influence job performance but here we’ll just assume that employers are able to measure all such things (not being able to do so would add additional variance to Job Performance, leaving effect sizes unchanged but reducing the magnitude of correlations everywhere).
Note that when looking at DAGs for causal inference we look at all possible paths, not just those where all the arrows point “the right way”. Hence the path (Test Performance → Got Hired ← Other Factors → Job Performance) is a valid way that test performance could potentially influence job performance and since we have two arrows pointing into “Got Hired” we see that getting hired is a collider for job performance. Hence the measured effect size if we control for getting hired (which e.g. only looking at those people who got hired) will not be the true relationship that doing well on the test has on doing well in the job.
We’ll also say that in our model 50% of the non-noise variance in job performance comes form general ability and 50% comes from all the other factors. Changing this number will slightly change the points of interest on our graphs later in the post but their general shape and theory behind what is happening is preserved, so WLOG we can make this assumption.
We’ll also say that both testing ability and other factors are normally distributed. Due to the Central Limit Theorem this is a good assumption of how such traits would behave in reality (because they are each composites of lots of different things). It also has the desirable property that all our composite measures (like the composite used to make hiring decisions and job performance) also end up being normally distributed and for simplicity we’ll rescale everything so that it has mean 0 and variance 1 (so a score of +1 on any measure means that particular individual is 1 SD above average on that particular thing).
3.
We are now ready to begin our analysis of the problem. In the ACX comments section, commenter
mentioned that the standard treatment of Berkson’s paradox is about how two things that are overall positively correlated with each other and both contribute to a third “performance” metric can show a negative relationship in a subsample selected to lie in a certain performance band.However the claim I was making was subtly different, I’ll reproduce the exact words I used:
This is because if there was a correlation then selectors would be leaving money on the table and they could improve their selection for the coming year by increasing the weighting on height (compared to everything else), which would in turn reduce the amount of correlation. Rinse and repeat until there is no correlation left.
Philip (correctly) mentioned that my claim was not that we’d get zero/negative correlation between the two components but rather that we’d see this between one of the components and actual performance, if the selection mechanism was properly calibrated. My general intuition was that this would still be true since we could imagine a continuum of selection processes, starting out with no weighting on ability (and therefore selecting on just Other factors) and increasing this weighting until we reach a point where our whole process just looks at ability and nothing else. In each of these cases we’d expect to see a certain amount of correlation between test performance and job performance which would be continuous function of how much the selection criteria weighted on test performance.
We can now model what we expect to see at different levels of weighting on ability. At zero weighting on ability we’d expect to see the full effect of ability on performance in the selected subset. Equally once we’re past the “true” weighting of 50% our selection criteria will start selecting people who have high test ability but are relatively worse on other factors.
This creates a situation where we’re selecting people with high ability but middling other factors, people with middling ability but exceptional other factors as well as some people who are very high in both of them, however because both our traits are normally distributed the relative amount of such people compared to those who are only high in one of them is very small, so they don’t influence the effect sizes/correlations very much. Thus we might very well see a negative effect size/correlation between ability and job performance.
Since the relation between weighting and effect size is continuous and it’s positive at 0 weighting and potentially negative at some point, by the Intermediate Value Theorem there would be a point where the correlation is zero. In my earlier comment I claimed that this zero would happen at the point where the selection criterion was perfectly calibrated with the actual contribution the factors made to job performance. It turns out (see later in the post) that this is not quite true, but with slight modifications a variant still holds.
Generally in analyses of Berkson’s paradox we look at the two components on the axes. Here I’m going to instead have the outcome on the Y-axis and show how Berkson’s paradox is modified for this situation and the cases in which it still applies.
4.
I created a Python simulation to check this hypothesis. My code can be found here, feel free to play around with the parameters and see how they change things. There are variables controlling how much noise we add to the test measurement (a noisy test will less perfectly capture actual ability, which is what influences job performance) and how much noise we have in job performance. Increasing these values above 0 will bias all correlations towards 0 and in the case of test measurement noise reduce the effect size but it won’t fundamentally change what we’re interested in so for what I present below I’m going to leave both of these at 0.
My simulation works by iterating over all possble differing weightings for test scores relative to other factors between [0,1] with an increment size of 0.01. The base step in my simulation generates two N-vectors of standard normals, representing test scores and other factors respectively. These represent N individuals where the i^th component of the first vector was the test score of the i^th individual and the i^th component of the second vector was their score on all other factors (I use N = 10,000 but this number is an optional input parameter for my code so easily changeable). Remember we’re normalising everything, so a score if +1 on the first compoent means this individual was 1 SD above average on the test.
Then I take the current test score weighting and compute a composite score. The composite I use is the following (w is the weighting):
where T is the score on the test and O is the score on other factors (both standard normals). This formula means that the composite C will also be a normal with mean 0 and variance 1 and that e.g. if w = 0.75 then a 1 unit increase in T will increase the composite as much as a w/(1-w) = 3 unit increase in O which tracks our intutions for what we expect to happen if test scores are 3x more important than other factors in getting hired.
I can also combine the two factors to compute the job performance for each individual. Since we’re saying that job performance is 50% captured by test performance and 50% by other factors we get:
(The 1/sqrt(2) factors are there to ensure that job performance still has variance 1.)
Once I have this done I then filter my sample to only keep those individuals whose composite score lies in the range I am interest in. I then run a regression to calculate the beta (effect size) and correlation between job performance and test scores on this subsample as well as the average level of job performance for this subset and compare it to the full unselected sample.
Since the results of a single trial have a lot of noise I repeat this basic step a large number of times for each weighting (I use 2500 iterations) and average out the beta, correlation and job performance of the selected subsample to get a single number for the effect size, correlation and performance boost as a result of slection for that particular weighting.
I then do this for all of the different weightings [0.00,0.01,0.02,…,0.98,0.99,1.00] and generate graphs of the observed mean effect sizes, correlations and performance boosts. On these graphs I can see the shape of how these things change as I vary the weighting of the selection process on getting hired, as well as whether there’s a point where the correlations become negative.
5.
First we look at a fairly standard analysis. I attempt to recreate my basketball claim. For this we’ll assume that the NBA only takes people who are at least 3 standard deviations above average on their selection criteria (roughly 1 in a thousand). The real NBA is a lot more selective than this but to ensure I had enough points in my selected subsample to do the regression I had to limit it here. Even then I’m having to raise my number of points per basic step from 2,000 to 100,000 for this. For the NBA analogy test performance would be the equivalent of height here.
This leads to graphs that look like this:
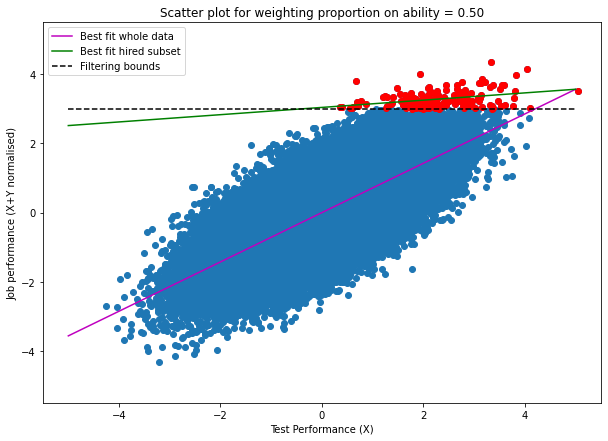
The blue dots are all the points, the red dots are the selected points (and the black dashed line is the boundary which separates selected from non-selected points. The purple line is the regression best fit of the whole data and the green line is the regression best fit of the selected points. From the title we can see this is using a selection method that has 0 weighting on test performance (here height).
We see from this that if our selection method doesn’t care about test performance (height), then in the selected subsample the effect size of having 1 unit more ability (or being 1 unit taller) is the same as in the whole population (the green and purple lines are parallel). This is exactly what we expect.
As we increase the weighting on test performance/height we start to see the correlation in our selected subsample reduce. Here’s what the graph looks like for weighting = 0.33:
The purple line is the same as last time (the dots themselves are different as I resample every time but the underlying distribution generating them is the same) but the green line is now less steep. This shows as expected that getting hired is acting as a collider for the link between test and job performnace and so if we only looked at the red dots our estimate of this effect (the gradient of the green line) would not match the true effect (the gradient of the purple line).
We continue increasing the weight on ability until we reach 50%. At this point our selection method is perfectly calibrated with actual job performance. We expect the dashed black line to be perfectly horizontal, and it is:
However interestingly the green line isn’t flat, it still has a positive gradient. This means that, counter to my claim in the original comment, at perfect calibration we still expect to see a positive link between test performance (height) and job performance (NBA results). This seems to contradict Berkson’s paradox: the effect size/correlation might be reduced, but it’s still positive.
All is not lost though, as we slightly increase the weighting on test performance beyond its optimal perfectly calibrated level we do indeed reach a point where the green line is flat:
and taking it even further from here (note that now increasing the weighting makes our selection criteria resemble the true combination that makes up job performance less and less) we can make it negative:
So it looks like yes, Berkson’s paradox is still valid: we can choose a weighting slightly above the optimal level and get our negative correlation.
If we continue increasing the weighting of test scores on the selection criteria we see something interesting happen. The green line starts rotating counterclockwise again until it returns to a positive gradient, returning back to the unfiltered effect size at weighting = 1 (the slight difference you see in the graph is noise):
The first time you see this it might look quite surprising, it seems beyond a point focusing your hiring process more and more towards the ability test (on height) and to the detriment of other factors leads to an increasing effect size of test ability on job performance of those hired. This is the opposite of what we were seeing at the beginning.
It might help to why this is happening if you just focus on the red dots in the last graph where ability weighting = 1. These are all the points where Test Performance >= 3, so our selected sub-sample is only those points where the test performance is above a threshold. However such a range restriction doesn’t change how important test ability is at influencing job performance, so of course we should expect to see the same effect size as on the full unfiltered sample. Then since we need our gradient to return to the same value at weighting = 1 that it was at weighting = 0 there must exist a turning point where it has to double back.
I must admit the first time I saw this initially I was surprised too and thought there must be a bug in my code. It was only after going through the above reasoning was I fully convinced that this was normal and expected behaviour.
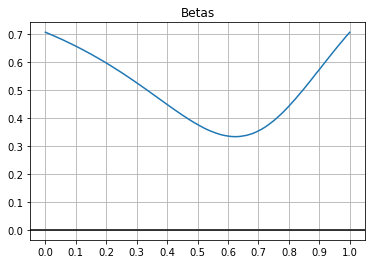
Overall if we plot the gradient of the green line depending on the test performance weighting it looks like this:
We see that at the beginning with weighting = 0 we see a strong effect size of around 0.7 (exact value should be sqrt(2)/2), so a 1 SD increase in test performance (height) of those hired corresponds to a 0.7 SD increase in their job (NBA) performance. As we increase this weighting the effect size goes down and at the point of perfect calibration between the selection criteria and the true job performance mix this effect size is merely 0.1 SD per extra SD of test performance (though still non-zero and positive).
Around weighting = 0.54 the effect size hits zero. At this point there is no effect/correlation between how well a hired person does on the ability test (their height) and how well they perform on the job (in the NBA). Increasing the weighting even further the effect size/correlation becomes negative, now for the average hired person a high performance on the ability test is overcompensating for potentially mediocre performance on other factors and the effect size reaches a minimum at weighting = 0.8 where beta = -0.54, meaning that at such a weighting level an extra 1SD test performance corresponds to an average 0.54 drop in job performance. Note that this difference is purely a statistical artifact of the selection process, the underlying reality is the same as for the unselected sample, namely that test performance is a very strong influence on actual job performance.
As we increase the weighting even further the effect size starts going back up, returning to positive values at weighting = 0.93 before returning to 0.7 at weighting = 1 as we now know to expect. So it looks like there is a “negative effect size well” between weighting = 0.54 and 0.93 where our selection process is forcing the measured effect of tested ability on job performance to be negative, even though in reality there is a strong positive effect.
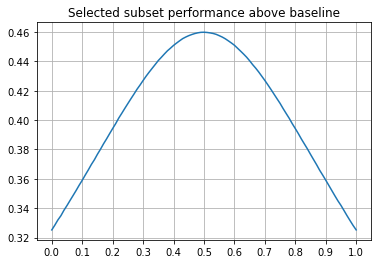
We also have a plot of the average improvement over baseline for each possible weighting. Higher numbers here mean a better filtering effect on actual job performance. It looks like this:
We see that we get the optimal filtering effect when our filter is perfectly calibrated with job performance. Note that the average effect at this optimum is slightly bigger than 3 SD because we’re taking everything >= 3SD so the average selected person will be slightly higher. As we move the weighting of the selection process away from this optimum the performance boost we get drops, although even when our process is all other factors/test performance we still get a ~2.3 SD boost to job performance.
Note that even in the “negative effect size well” the selection boost is between 2.4-3.25, which is higher than the selection boost of a process that doesn’t look at test performance at all. For example a selection process that puts a 60% weighting on test performance would show a measured effect size of -0.15 SD increase in job performance per SD increase in test ability among the hired but give a selection boost of about 3.2SD, which is significantly higher than if weighting = 0 (only 2.3 SD).
So the basic premise behind Berkson’s paradox and its applicability to hiring processes still holds: there are still large regions of weightings on test performance which lead to a better selection effect compared to ignoring test performance completely but show negative measured effect sizes/correlations amongst those hired.
Hence the claim in my original comment (though not the exact reasoning) is still true: just because an analysis test scores vs of on the job performance of those hired doesn’t show a positive relationship doesn’t mean that the test isn’t measuring something important or isn’t adding direct tangible value in leading to the company hiring more suitable employees.
While it may be true that at perfect calibration we still see a positive correlation/effect size if the filtering process is even slightly overweighted towards ability tests we get negative correlation just like as in the standard treatment of Berkson’s paradox. Regardless, even these overweighted filtering processes are better at selecting a subsample that does well on Job performance than a selection method which ignores the test completely, hence the tests are adding genuine value to the selection process.
6.
I’ll make a quick digression here to talk about correlations, or rather talk about why I didn’t talk about correlations much in the last section and instead chose to focus on the effect size. Personally I’m not a big fan of correlations (or r^2 or associated r^2 like objects such as genetic heritability) and think they have a great tendency to confound understanding rather than help it and that this is especially true for people who aren’t particularly knowledgeable about statistics. I think our case provides one very good example of why correlations can be very misleading more generally.
We can make a graph of the correlations for each weighting and plot it just like we did for the effect size. That gives the following:
We see that the correlation starts out very close to 1, drop down to negative values at the same time as the effect size and recovers to a positive value as the weighting moves closer and closer to 1. However even when we’re at weighting = 1 the correlation is much less than the correlation at weighting = 0. This is different to the effect size, which returns to the same value at weighting = 1 that it was at weighting = 0.
Instead the correlation only makes it back to about r = 0.25. For reference the correlation between test scores and job performance on the full unfiltered data is r = sqrt(2)/2 = 0.7 . So it looks like when we’re filtering completely on other factors our measured correlation between test scores and job performance is much higher than on the full data while when we’re filtering completely on test scores the measured correlation is much lower, even though the effect size for all three of these cases is exactly the same (0.7). Put in simple terms the measured correlations are very different for the three cases even though the measured effect size for all of them is +0.7SD job performance for every 1SD increase in test scores.
This can seem very strange initially until you remember that we can think of the square of the correlation r^2 as the percentage of variance in the dependent variable explained by the variance in the independent variable. We can write the r^2 as follows:
Note that this is an increasing function of the “Test” variance and a decreasing function of the “Other” variance.
In the weighting = 1 case we are selecting our subsample to be high on test scores so the amount of variance in test scores present in the selected subsample is much smaller than the amount of variance present on the same factor in the full data. We can see this on the graph (reproduced below); the projections of the red dots on the X-axis cover a much smaller range than the projection of all the data points:
This means the amount of variance in test scores we have on our filtered subsample is a lot lower than the amount of variance in test scores on the whole data. While the amount of variance in “Other” is unchanged (since our filtering mechanism doesn’t select on it). Hence our r^2 is lower than what it would be in the full unselected data and this is indeed what we see.
Equally when weighting = 0 our selection process is based completely on other factors and not test scores. So in the selected subsample the “Test” variance will be unchanged but the “Other” variance will be much smaller. Plugging into the formula this leads to a much higher overall r^2 compared to the unselected case and is exactly what we see. Note that the graph for weighting = 0 doesn’t directly help us see this much because neither the X nor Y axes represent “Other Factors”; the line representing “Other Factors” is instead the perpendicular to the dashed black line and if we project the red dots on that line we do indeed see the subsample variance is very low.
Since r^2 is so different for all the three cases it follows that its square root, r, the correlation, will also be different. Here we see quite clearly why the correlation is a bad metric and confusing: even though in all three cases the marginal impact of better test scores on job performance is the same we get very different correlation numbers.
It’s made even worse because less statistically inclined people often use a table like this:
to interpret the relationships they see. According to this table the relationship between test scores and performance is weak when we look at a subsample selected only on Test Performance, strong when we look at the whole data and very strong when we look at a subsample selected only on Other Factors, even though, and I can not stress this enough, the effect size of the relationship between the two (which is what tells us how much an extra unit on one thing changes the other) is the same in all three cases!
As a society we’d be a lot better off if we forgot completely about correlations and r^2 (not saying they are useless; they have their uses but it has to be done judiciously). That way we’d have a lot fewer cases of people interpreting effects that are in reality very strong as being weak (because the magic correlation number said so) and vice versa. Instead we should be focusing on the standard deviation scaled effect sizes of relationships instead. Like the correlation and r^2 this too is a unitless quantity and is much easier to correctly interpret: a SD scaled effect size of 0.25 of A on B means for a 1 SD increase in A we expect to see a 0.25 SD increase in B. For our example above this number is 0.7 in all three cases and correctly showcases that e.g. just because you select a subsample based on high test scores it doesn’t mean that test score performance starts mattering less for job performance.
For this reason I’m going to keep discussing effect sizes instead of correlations for the rest of my post.
The public’s general understanding of statistics would be a lot better if the classes on linear regressions general students take stopped talking about correlations and “percentage of variance explained” and instead spent the saved time discussing the standard error of the estimates from linear regression. However now we’re starting to digress from our main topic and my ideal statistics class for non-mathematicians is a topic for another day.
7.
We’ve seen so far that if we have a very strong filtering effect Berkson’s paradox still applies. Plenty of comments on the main post mentioned that the vast majority of companies don’t filter their hires to be at the very top of the distribution but instead only do simple baseline testing. This would lead to lower changes in the effect size as we vary the weighting of test performance on the selection process.
However for such companies we have an additional effect where applicants who are too good instead choose to go work elsewhere for better pay/progression/prestige etc etc., so in the end the hired subset is not all applicants that meet a threshold but rather applicants whose scores on the hiring criteria lie within a band. This band being thinner and thinner once again increases how much the effect size changes as we change our weighting criteria.
In fact the results in such a case aren’t particularly different. The shapes of the curves look remarkably similar, the only thing that changes is the values on the Y-axis. For instance if we were to look at a case where the company was willing to hire anybody average or better (selection score > 0) but people +1 SD or more above average instead chose to go work elsewhere we‘d get a case where the selected group would look something like this:
And the effect size and selection strength graphs look like:
which as we can see are very similar to the case where we were only filtering for the very top of the distribution. In particular the “well of negative effect sizes” is still there in basically the same place and even in this well the selection strength is more than the selection strength if our process ignored test scores completely (weighting = 0).
The next question to ask is that if there was no upper limit how strong does the selection effect have to be to get the well of negative effect sizes? For instance if we select just the top half on our selection metric (so Combined score >= 0) like this:
then the effect size never becomes negative:
In such a case no matter how much the selection process weights test performance the measured effect size between tests and job performance stays positive. In fact even a > 1 SD selection criteria isn’t stringent enough to create the well of negative effect size:
We have to go all the way until C >= 1.25 to get a situation where the measured effect size just about hits 0. If our selection is at least this stringent we get to see Berkson’s paradox with the outcome as our dependent variable, otherwise while we see a reduction in the effect size (and yes, correlation) it still stays positive:
8.
Putting the whole post together we can make the following conclusions:
If an employer hires people based on a combination of test scores and other factors then getting hired is a collider for job performance. This means the measured linear regression effect of how test scores affect job performance won’t show the true effect.
The classic Berkson’s paradox shows how your test performance can be uncorrelated to other factors in the whole population but have a negative relationship amongst those hired.
We can also look at the relationship between one factor and the outcome measure (job performance). This relationship will change as we change the relative importance of test scores vs other factors.
Initially as we increase our weighting from 0 the magnitude of the effect size test scores have on job performance among those hired will reduce. However as the weighting gets very large and our selection criteria become closer and closer to just an ability test the effect size will go back up to the level it would have been in the full population.
If our criteria is stringent enough we can create a “well of negative effect size”, a region of weightings where the measured effect size of test performance on job performance among the hired is negative, even though the true effect is positive.
Even inside this region the level of increased performance we get from the selection is more than what we would get from a process that was just as stringent but didn’t look at test results at all. Hence the test result is still adding meaningful and useful information to the process even though the measured effect of the test on job perforance for those hired is negative.
Correlations are generally a very poor way to look at the strength of a statistical relationship. They normally introduce more confusion and potentially lead to incorrect inference than they normally help. It’s much better to use alternative metrics like the standard deviation scaled effect size. (This is so important and relevant to not just this post that I’ve bolded it).
We see Berkson’s paradox with the outcome measure not only for very strict filtering at the top end but also in cases where we have moderate filtering at the low end but high performers choose to go work elsewhere. The smaller the band of combined scores between the point that the company is willing to accept and the point where people are able to get hired somewhere better the stronger the effect we see.
If the selection criterion is too weak and there’s no upper limit after which people start leaving to work elsewhere then there’s a minimum selection strength we need to see the paradox. A less stringent requirement will show reductions in effect sizes but it will stay positive over the full range of weightings on test performance.
To wrap it up I’ll leave you with a quick video of all the scatter plots for when we’re selecting the subsample between 0 and +1 SD showing how the data and the line of best fit (and effect sizes) change as we vary our weighting on test scores:
Once again thanks to commenter
for engaging me in discussion on the Astral Codex Ten post, without which I would never have thought about investigating this problem in anywhere near this much depth in the first place.The basketball claim:
Some people asked about my source for this info about height being uncorrelated with performance in the NBA. A commenter pointed out that there’s a 2020 study that looked at FIBA World Cups and found that players in higher performing teams tended to be taller. I personally don’t consider this to completely falsify my claim because 1) FIBA tends to be less prestigious than the NBA (see how the US keeps sending comparatively less well known athletes to the FIBA cups) so these athletes aren’t at the very top of the top, 2) The authors of the study found no relationship between height and team performance for the 2 tallest of the 5 positions and 3) The author’s don’t seem to have corrected for multiple hypothesis testing and 2 of their 3 positions which showed a significant effect had 0.01 < p < 0.05 . However it’s still something to be aware of.
My sources for the NBA claim come from analysis done previously by Thomas Vladek here which includes the following tweet:
I recommend reading Thomas’s article as it covers similar stuff to what we’ll be doing today, although we’re going to be looking at things from a somewhat different angle. There are also tweets by other people who did the same analysis and came to similar conclusions:
The obvious confounder here is that not all basketball positions are equal in how often they score or how tall the people at that position tend to be. In fact the shortest/second shortest position (Shooting Guard) tends to score the most while the tallest position (Center) tends to score the least . This would then suggest that unless we further break down the results by position the two results above don’t really mean much at all. However there are other papers that did an analysis and found that controlling for position a player’s height doesn't matter in how well a team does in the NBA. They do have some subgroup analyses (Regular Season vs Playoff/Western Conference vs Eastern etc.) where height does seem to matter but they all have lackluster p-values and about half of them show smaller height teams performed better to the point that I don’t consider any of them to be indicative of a general trend. All in all I still stand by my claim but would caveat it with “other analyses that have found otherwise also exist”.























My informal goto example to explain this to co-workers is:
If you look at multiple people's CVs, you expect the ones with more typos to be less impressive.
But if you restrict yourself only to people who worked at Google, you expect the guy who got hired despite lots of typos to be rather exceptional.
Similarly, Matt Levine wrote that you should expect hedge fund managers who look the least like hedge fund managers to do best.
well done